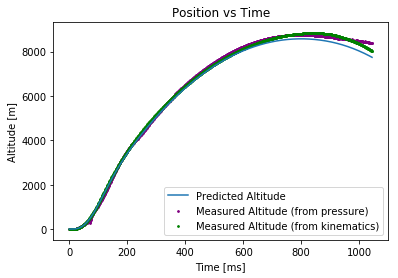
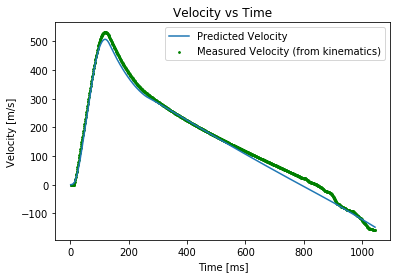
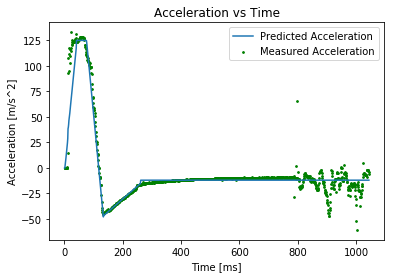
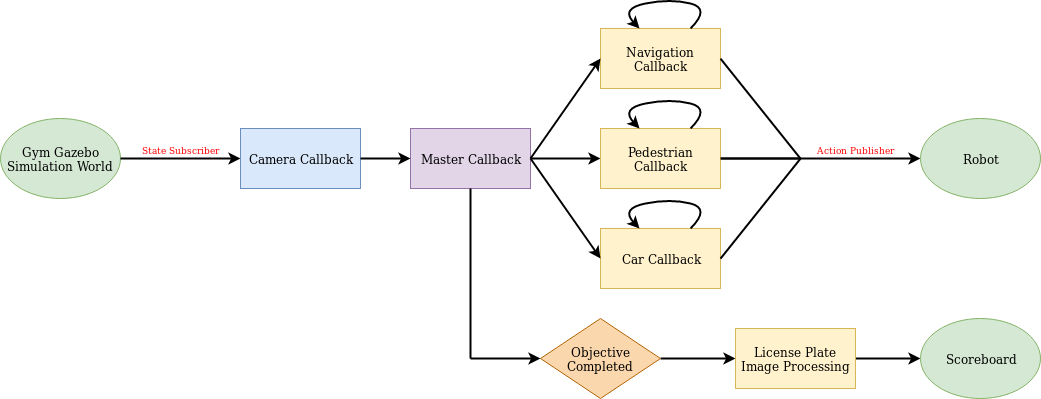
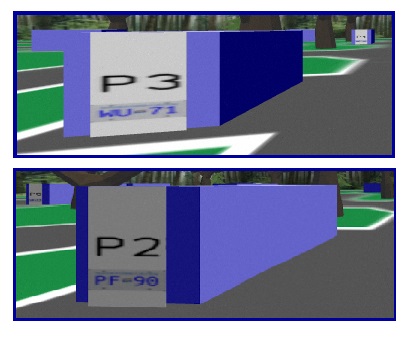
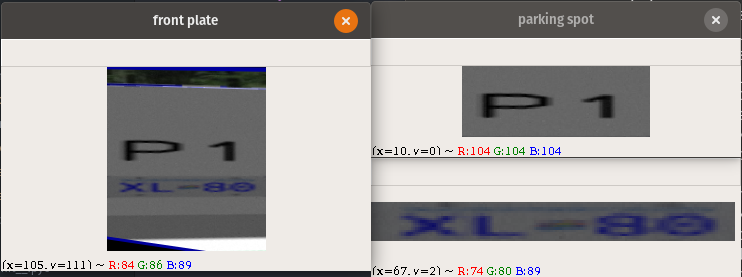
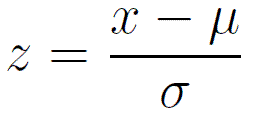About

Through a diverse range of work experiences, club and design team involvement, and participation in multiple competitive team sports growing up, I have developed a powerful perspective on the impact a dedicated, cohesive team can have. As I continue to expand my skillset and familiarity with some of the new advancements at the forefront of the tech industry, I am excited to find meaningful projects with people who share my interest and enthusiasm in making an impact, and affecting positive change in our communities.
I am currently a fifth-year Engineering Physics student at The University of British Columbia in Vancouver, BC. I am working towards a specialization in computer science, and a minor in statistics, and I expect to graduate in April, 2022. Feel free to reach out to me at any time, I would love to chat about some of the awesome projects and teams I have been (or am still) a part of!
A PDF of my current resume can be found at the following link.
Ben Huckell - Resume 2021



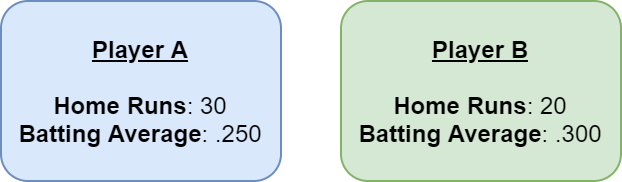
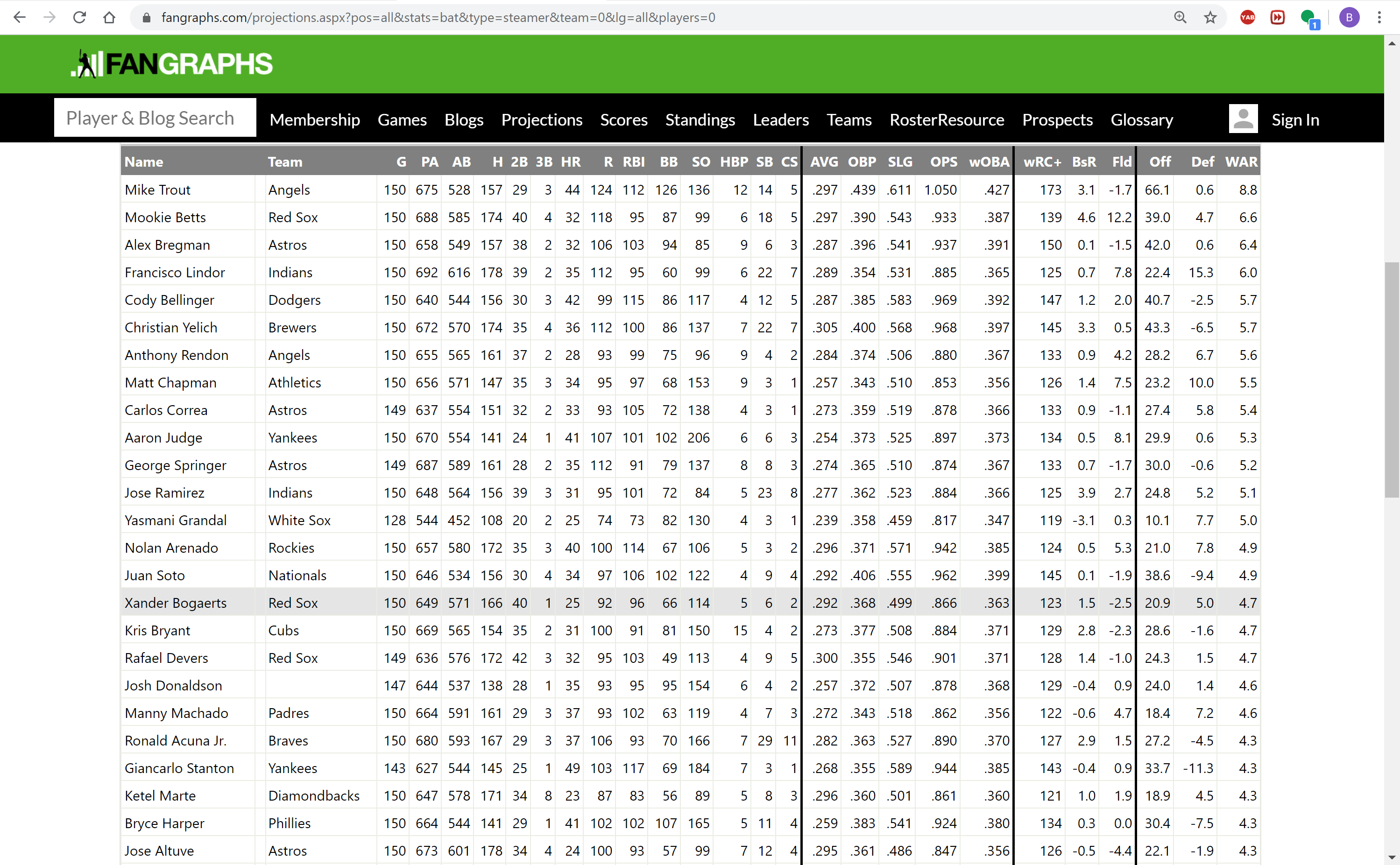
.jpg)